안녕하세요 공돌이 김넙죽입니다!
오늘 풀어볼 문제는 2021학년도 수능 9월 모의고사 수학 가형 28번입니다.

이렇게 도형을 주고 극한을 구하는 문제는 매년 나오는 단골 문제이죠. 이 유형이 어려운 이유는 크게 두 가지입니다.
1. 도형을 분석하여 주어진 식을 세타에 대해 나타내는 과정
2. 구한 식의 극한값을 구하는 과정
이 두 과정 모두 제대로 해내야지만 정확한 답을 구할 수 있죠. 이 때문에 매년 수능에서 18~21번 구간, 또는 27~30번에서 빠지지 않고 나오는 유형입니다! 그렇다면 이러한 문제를 풀기 위해 어떠한 방법을 사용할 수 있을까요?
첫번째는 우선 문제를 단순화시키는 것입니다. 보통은 분모에 θ가 오는게 일반적인데, 지금 식은 RH가 있죠? 따라서 먼저 RH를 θ에 대해 표현해보는게 다루기 더 쉬워지겠죠! 각 QPB=θ이므로 RH=PRsinθ가 되며, 삼각형 PRO에서 사인 법칙을 쓰면 PR=sin3θ/sin(5θ/2)이므로 결국 RH는 6θ/5로 근사시킬 수 있는 것이죠 :)
결국 주어진 식은 θ에 대한 두 영역의 넓이 합의 비를 가리킵니다. 이때 삼각형 POB와 부채꼴 QOB의 넓이가 각각 1/2×sinθ와 θ라는 것은 쉽게 알 수 있는 사실인데, θ가 0으로 가므로 이 두 값은 θ/2와 θ로 근사시킬 수 있죠. 따라서 삼각형 ORB의 넓이를 θ에 대해 표현하는 것이 우리의 최종 목표가 되는 것입니다!
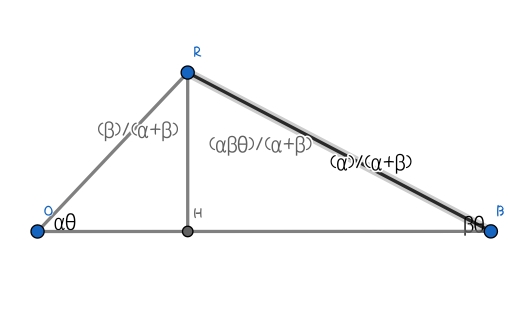
θ가 0으로 가면 그림처럼 각 변을 근사 가능하게 됩니다. 따라서 결국 삼각형 ORB의 넓이는 θ/5가 되는 것이죠. 이를 통해 f와 g를 계산하면 f=3θ/10, g=4θ/5가 되는군요! 이를 통해 답을 계산하면 11/12가 나오게 됩니다 :) 이상으로 근사를 통한 극한값 계산 방법이었어요~공돌이 김넙죽이었습니다:)
'수능 수학 풀이' 카테고리의 다른 글
| 2021학년도 수능 6월 모의고사 - 가형 28번 (3) | 2020.10.05 |
|---|---|
| 2021학년도 수능 9월 모의고사 - 나형 25번 (1) | 2020.10.04 |
| 2020학년도 9월 고2 전국연합학력평가 수학 - 27번 (8) | 2020.10.02 |
| 수능 수학 풀이를 작성해보려 합니다! (0) | 2020.10.02 |



댓글